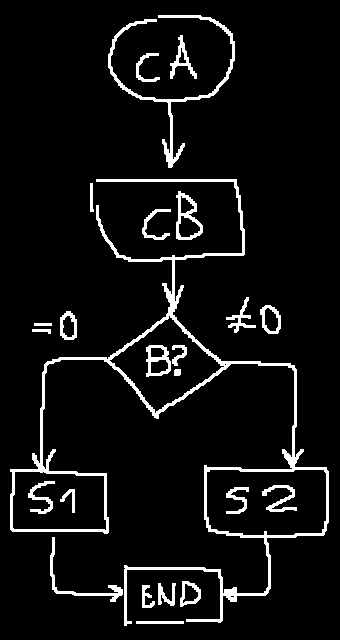Commento del diagramma 1) Calcolo di A 2) Calcolo di B 3) Condizione su B 4) Eseguzione di uno dei due flussi 5) Fine Per eseguire S1 o S2 debbo avere calcolato il valore A Per eseguire la condizione su B devo eseguire il calcolo su B

 Calcolo il tempo impiegato da una CPU per eseguire il programma:

 Dove T( ) e p( ) sono rispettivamente il tempo impiegato e la probabilità che accada.

 Inoltre p(S2) = 1 - p(S1) essendo le due condizioni mutuamente esclusive.

 Ora calcolo il tempo impiegato da un doppio processore, ma prima occorre indrodurre alcue considerazioni [nota 1]:

- si suppone che quando due processori eseguano in modo concorrente lo steso processo essi impieghino meta` tempo di un procesore singolo. Questa ipotesi e` lecita finche` si vuole indagare se vi sia la possibilita` di ottimizzare il multi-thread in modo da ottenere una prestazione maggiore del 200% rispetto al singolo processore.

- si semplifica immaginando che le due CPU non debbono concorrere all´accesso della memoria, dei dischi o di altre risorse si sitema (valutazione sulla potenza bruta di calcolo).

- si semplifica immaginando che la CPU 1 elabori il calcolo B e la CPU 1 elabori S1 e/o S2 e che una CPU intervenga in aiuto dell´altra solo nel caso che abbia finito il proprio compito.

 Le ultime due ipotesi sono delle maggiorazioni atte a semplificare il calcolo. In definitiva se anche con l'uso di tali maggiorazioni (delle prestazioni) non si supera il limite lineare allora questo è non falsificato (almeno da questi calcoli).

 In particolare nelle ipotesi precedenti ho ignorato i seguenti fatti che riducono le prestazioni:

- Le risorse di sistema, come la quantità di RAM, siano più sufficiente per entrambe le CPU.

- Overhead dovuto al riassegnamento dei compiti alle due CPU.

La terza ipotesi è più delicata e contiene due parti separate:

- Si suppone arbitrariamente di poter chiamare un set di istruzioni "processo singolo"

- Il "processo singolo" è eseguibile in modo concorrenziale al 200%

 La seconda parte è una maggiorazione introdotta per le medesime ragioni delle altre due.
 Mentre la prima parte è una convenzione introdotta con il seguente scopo: "l'intero programma può essere pensato come un processo singolo eseguibile al 200% ma se lo suddivido in maniera intelligente in diverse porzioni e predispongo per le diverse porzioni diversi modi di gestire il multi-thread allora posso ottenere prestazioni superiori".

 Facendo uso delle ipotesi sopra dette calcolo il tempo impiegato da un doppio processore

 Il termine T(*) e` diverso a seconda che si impongano delle condizioni su T(cB), T(S1) e T(S2):

1. Nel caso che T(cB) > T(S1) + T(S2) capita che la CPU 2 finisca prima della CPU 1 ed a questa venga in soccorso per completare il lavoro:
   

       
   T(2cpu) = T(cA)/2 + T(S1) + T(S2) + [ T(cB) - T(S1) - T(S2) ]/2
       

   
   
2. Nel caso che T(cB) = T(S1) + T(S2) capita che la CPU 2 finisca esattamente quando la CPU 1 e non vi sia alcuna collaborazione:
   

       
   T(2cpu) = T(cA)/2 + T(S1) + T(S2) = T(cA)/2 + T(cB)
       

   
   
3. Nel caso che T(cB) < T(S1) + T(S2) capita che la CPU 1 finisca prima della CPU 2 a questo punto possono capitare ancora 3 cose:
   
   
   • la CPU 2 non ha completato entrambi flussi ma ha completato quello che serve:

             
     T(2cpu) = T(cA)/2 + T(cB)
             

   • la CPU 2 deve completare la sequenza che serve:

             
     T(2cpu) = T(cA)/2 + T(cB) + [ T(cS) - T(cB) ]/2
             

   • la CPU2 deve ancora iniziare il calcolo della sequenza che serve:

             
     T(2cpu) = T(cA)/2 + T(cB) + T(cS)
             

   Appare evidente che la prima di queste tre evenienze e` la piu` favorevole mentre nella terza il lavoro della CPU 2 e` andato totalmente perduto.

 Per controllare l´esistenza deil limite teorico del 200% si esegue il controllo del segno sul seguente valore

 Sostituendo il valore T(*) secondo i punti 1, 2 e il primo del 3 ottengo rispettivamente:

1. DT = Tmed(Sx) - T(S1) - T(S2) < 0 per la proprieta` della media

   
   

2. DT = Tmed(Sx) - T(cB) < 0 perche` T(cB) = T(S1) + T(S2)

   
   

3. DT = Tmed(Sx) - T(cB) con T(cB) < T(S1) + T(S2)

   
   

 Quindi solo il punto 3 ha qualche speranza di superare il rendimento del 200% e questo si verifica per la seguente condizione:

• T(cB) > T(cS) > Tmed(Sx)

ora il mssimo rendimento si ha quando T(cB) = T(cS). Ora accade che

• se T(S1) e T(S2) non hanno lo stesso valore allora il miglior rendimento si ha per

       
  T(cS) = p*T(S1) + (1-p)*T(S2) = Tmed(Sx)
      

  per l´ovvio motivo che e` per definizione il valore che meglio approssima i due;

  
  
  
• altrimenti se T(S1) = T(S2) per la proprieta` della media accade che

       
  Tmed(Sx) = T(S1) = T(S2) e quindi ancora che T(cS) = Tmed(Sx).
      

 Con questo si dimostra il limite teorico per cui due processori in parallelo non possono produrre un rendimento superiore al 200% di un singolo processore.

 Poichè ci sono degli esempi pratici in cui il limite lineare del 200% è stato superato significa che le ipotesi da cui si è dedotto questo limite non valgono sempre.
 Ad esempio quando il carico di lavoro è troppo pesante per essere affrontato da un'unica CPU, ma non da due, allora la prestazione risulta affetta da sovraccarico e il rapporto con questa misura esula dal limite teorico).
 Quest'ultima considerazione puè essere paragonata a quanto previsto dalla legge di Ohm: per un generatore di tensione ideale ci si aspetta che la corrente sia linearmente proporzionale alla conduttanza. Sappiamo bene invece che i generatori reali si comportano linearmente solamente entro un range di conduttanza al di fuori del quale perdono la capacità di fornire una prestazione lineare (corto circuito V->0, A->oo ma cmq Pw = VA = cost).

(continua...)